Water Water everywhere!

About this lesson
In this lesson, students are presented with the challenging problem of measuring a volume of water using containers that are not the exact measurement size. Students will decompose a complex problem into discrete steps, design an algorithm for solving the problem, and evaluate solution efficiencies and optimisation in a simulation.
Year band: 3-4, 5-6
Curriculum LinksCurriculum Links
Links with Digital Technologies Curriculum Area
| Year | Strand | Content Description |
|---|---|---|
| 3-4 | Processes and Production Skills |
Define problems with given design criteria and by co-creating user stories (AC9TDI4P01) Follow and describe algorithms involving sequencing, comparison operators (branching) and iteration (AC9TDI4P02) |
| 5-6 | Processes and Production Skills |
Design algorithms involving multiple alternatives (branching) and iteration (AC9TDI6P02) |
Links with Mathematics Curriculum Area
| Year | Strand | Content Description |
|---|---|---|
| 3-4 | Measurement |
Interpret unmarked and partial units when measuring and comparing attributes of length, mass, capacity, duration and temperature, using scaled and digital instruments and appropriate units (AC9M4M01) |
| 5-6 | Measurement |
Choose appropriate metric units when measuring the length, mass and capacity of objects; use smaller units or a combination of units to obtain a more accurate measure (AC9M5M01) |
Learning hook: The challenge (15 minutes)
In this activity, students will be faced with the complex problem of measuring 5 mL of water with only a 4 mL container and a 7 mL container. Students must use decomposition to break the problem into smaller problems and then to design an algorithm to solve it.
Activity:
Ask students to solve the following problem:
You’ve run into a predicament. You want to do a science experiment. Given two containers, one that can hold 4 millilitres and one that can hold 7 millilitres, how can you get one of these containers to hold exactly 5 millilitres?
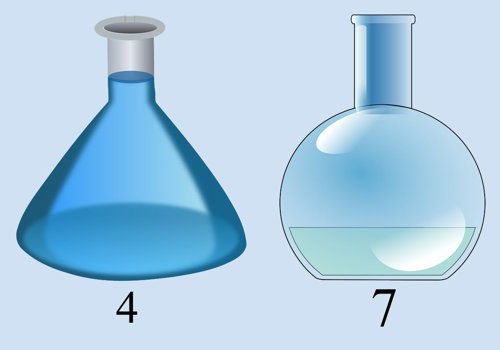
Notes to the teacher:
Tell the students the containers are blacked out and oddly shaped, so you can’t tell by weight or watermark how much is in the container - you can only accurately tell if it is empty or if it is full. You can’t look at the container to ascertain any other quantities.
You may notice that some students need help to get started. Stop their work and ask, “What do you know about the final desired volume?” “How can you express that value other than ‘5’?” “How do you think you can break this big problem into smaller problems?”
Assessment:
Ask students how they came up with the process for determining the correct solution. After the discussion, continue to Activity 1 in which you will suggest decomposition as a starting point.
Learning input: Pour the water (20 minutes)
In this activity, students will use decomposition to break down the problem into discrete steps and use the set of steps to design a method, or algorithm, to measure 5 mL of water.
Encourage students to describe the solution in discrete steps and to record the amount of water in each container (A and B) contains at each step.
We can do this by first noting that at any point there are only three actions we can do: completely fill a container, completely empty a container, or move the contents of one container to another (for this, we can use the shorthand A -> B to mean pouring the contents of A into B).
So an instruction to fill up the first container (A), pour it into the second (B) and then empty container B would look like:
| Instruction | Quantity in A (max 4) | Quantity in B (max 7) |
|---|---|---|
| START | 0 | 0 |
| Fill A | 4 | 0 |
| A -> B | 0 | 4 |
| Empty B | 0 | 0 |
Learning demo: Pour the water (20 minutes)
In this activity, students will use decomposition to break down the problem into discrete steps and use the set of steps to design a method, or algorithm, to measure 5 mL of water. Finally, they will execute a simulation to test their algorithm for optimisation and efficiency.
Once students are comfortable with the notation, allow them to create their own table to describe the solution by interacting collaboratively in small groups.
An example solution might look like:
| Instruction | Quantity in A (max 4) | Quantity in B (max 7) |
|---|---|---|
| START | 0 | 0 |
| Fill B | 0 | 7 |
| B -> A | 4 | 3 |
| Empty A | 0 | 3 |
| B -> A | 3 | 0 |
| Fill B | 3 | 7 |
| B -> A | 4 | 6 |
| Empty A | 0 | 6 |
| B -> A | 4 | 2 |
| Empty A | 0 | 2 |
| B -> A | 2 | 0 |
| Fill B | 2 | 7 |
| B -> A | 4 | 5 |
If students find a valid solution, encourage them to find other solutions to the same problem. Ask them to count the number of ‘instructions’ used by their solution (for example, the number of instructions for the above would be 12). Explain that the number of instructions used can be taken as a measure of the optimisation or efficiency of their solution - the lower the number, the more efficient the solution because it takes fewer operations to achieve the goal.
A more efficient solution (because it only uses 9 instructions) would be:
| Instruction | Quantity in A (max 4) | Quantity in B (max 7) |
|---|---|---|
| START | 0 | 0 |
| Fill A | 4 | 0 |
| A -> B | 0 | 4 |
| Fill A | 4 | 4 |
| A -> B | 1 | 7 |
| Empty B | 1 | 0 |
| A -> B | 0 | 1 |
| Fill A | 4 | 1 |
| A -> B | 0 | 5 |
Assessment:
Assess students on their ability to reach the correct answer. Assess higher-level students on finding the most efficient/optimal method (the fewest number of steps).
Learning reflection: Assessment (10 to 20 minutes)
In this activity, students analyze their method for measuring 5 mL to determine: a) how they figured out how to start - decomposition, b) how they worked out the solution - algorithm - to solve the problem, and c) if their method is efficient based upon testing a simulation. Finally, they solve a similar problem and their solution is assessed.
Activity:
Give students the task of optimizing the algorithm they designed.
Assign a similar problem with different sized flasks of water and a different goal. If they have learned a process for solving this type of problem, they can apply the process to a different scenario.
Q1: How do you know how to start?
Q2: How do you know if you should use the method that pours A into B or the method that pours B into A?
Assessment:
Assess student answers to a new problem or assess optimisation strategies.
A1: You know that you do not have a 5 mL container, so the only way you can get 5 is by adding two smaller components like 4 and 1 or 2 and 3, for instance. The only way you can get 1 mL, 2 mL, or 3 mL of water is to mix and pour water from one container into another.
A2: Generally speaking pouring the smaller container (4) into the larger container (7) gets you to the amount of 1 mL much faster which is helpful if you want to add it to 4 mL in order to get 5 mL, the goal.
Additional information and resources
Lesson Vocabulary
| Term | Definition | For Additional Information |
|---|---|---|
| Optimisation | The process of modifying a software system to make some aspect of it work more efficiently or use fewer resources. | |
| Complexity | Characterisation of something with many parts where those parts interact with each other in multiple ways, or the degree to which something can be characterised in this way. |
Computational Thinking concepts
| Concept | Definition |
|---|---|
| Decomposition | Breaking down tasks into smaller, manageable parts |
| Algorithm Design | Creating an ordered series of instructions for solving similar problems |
| Simulation | Representing or modeling a process |