Making maths quizzes 1: Plan and test our programs
About this lesson
In this sequence of lessons students plan, create and edit a program that will ask maths questions that are harder or easier depending on user performance.
Year band: 5-6
Curriculum Links AssessmentCurriculum Links
Links with Digital Technologies Curriculum Area
| Strand | Content Description |
|---|---|
| Processes and Production Skills |
Design algorithms involving multiple alternatives (branching) and iteration (AC9TDI6P02). Implement algorithms as visual programs involving control structures, variables and input (AC9TDI6P05). |
Links with other Learning Areas
| Learning Area | Strand and Content Description |
|---|---|
| Mathematics | Number and Algebra Solve problems involving multiplication of larger numbers by one- or two-digit numbers, choosing efficient calculation strategies and using digital tools where appropriate; check the reasonableness of answers (AC9M5N06) |
Assessment
Assessment for learning
Anecdotal discussion around students' prior knowledge concerning both the key terms about and the functionality of the program.
Assessment as learning
- Observation of student teamwork
- Student self reflection, comparing their understanding of the key concepts with those displayed on the answer sheet
- Students self-reflect using the rubric as a guide. They colour the rubric in yellow to show where they think their level is.
Assessment of learning
- Final copy of group's plan.
- Use of the student assessment rubric by the teacher. The teacher colours in the same rubric that the students have used, but this time blue for their mark.
Learning hook
- Introduce the sample PowerPoint (or alternative such as Keynote for Mac or Google Slides) as a game to the students. Use the interactive whiteboard, or TV, and then have students take it in turns to try and answer the question. (Note: You will need to have it in 'slide show' mode). Give students a time limit for each answer. Once they have had at least one turn each, explain that they are going to learn how to make a program exactly like this.
- If you are dealing with a particularly large group size, or are concerned about the students not being engaged watching each other take turns of the quiz, a possible solution is to model on example quickly, and have multiple computers set up with the quiz so that students can work through it in small groups of 3–5.
Learning map and outcomes
Tell students:
- 'In this lesson is that we are learning to plan, create and then edit a program that will ask you maths questions that are harder or easier depending on how well you are going. We are going to learn to plan and test our programs so that we are ready to make them digitally. This is only the first of two lessons. We will complete a plan for our program by the end of this lesson, and create the program itself in our next lesson.'
- Break this sentence down with them and discuss what skills they will need in order to be able to achieve this goal. Say: 'What do you need to be able to do to plan and test a program?'
- Hand out the assessment rubric and briefly go through it with them.
- Get the students to discuss it with the person next to them and write notes on the rubric in their own words to help them understand what is expected of them.
- Explain to students that they will use this to guide their work and that they will have a greater understanding of each section as they move through the lesson.
Learning input
- Ask the students to think about how they think this program is working, and what is going on behind the scenes. Give them 5 minutes to discuss this with the people next to them.
This is essentially a Think, pair, share with some guiding questions.
- What does this program need to function?
This is a question that they most likely will not be able to answer, and will struggle with. This is ok, the goal is to get them starting to think about programs as having a 'back end', and helping them to be more receptive to the idea that there is more going on than meets the eye. - Once they have finished discussing the idea, explain that each different thing that they have seen on the screen is a different slide in a PowerPoint presentation.
- Ask them if this helps them visualise what is going on.
- Next, ask them whether they can think of any way to plan this, or draw it in a way that would represent what is happening.
- Let them have 5 minutes to draw or jot down some ideas.
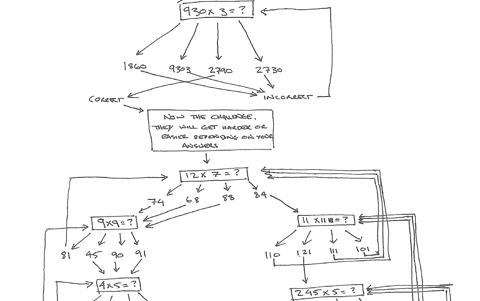
- After 5 minutes display the diagram provided that shows the relationship between the slides.
This diagram may look rather confusing and scary but it is actually really simple, and it is worth explaining this to the students to help them to engage with it confidently.
- Now is the time for you to explain to the students the four concepts of 'IF', 'OR', 'Iteration' and 'Branch'.
- An 'IF' statement is a conditional statement, it is a choice. An IF statement tests whether something is true or not. 'You ate chocolate today.' is an example of an IF statement. IF you have then the statement is true. IF you have not then it is false.
- An 'OR' statement is where two or more responses have the same result. If a question has two right answers, then answer A OR answer B could be selected and still be correct. This also applies if there are two or more wrong answers.
- 'Iteration' means the same thing as 'repetition'. If there is an iteration of something, then it goes back to its beginning and starts again.
- 'Branch' means when something has more than one possible option that stems from it. This is like the branches on a tree, it starts with the trunk but you can then choose to follow one of any of the other branches that break off from it.
- An 'IF' statement is a conditional statement, it is a choice. An IF statement tests whether something is true or not. 'You ate chocolate today.' is an example of an IF statement. IF you have then the statement is true. IF you have not then it is false.
- Ask the students to discuss with the person next to them where they think they can see examples of each of these in the diagram in from of them.
- After a short discussion demonstrate where to find an example of each in the first instance of equations on the diagram. Have students step through the diagram by using their finger to point out the different concepts in the diagram.
- Once it is clear that the students have a basic understanding of these three concepts, provide them with one copy of the handout of the diagram between two, and ask them to label every relationship between slides in the diagram as one of these three terms.
- After a short discussion demonstrate where to find an example of each in the first instance of equations on the diagram. Have students step through the diagram by using their finger to point out the different concepts in the diagram.
- Show them the answer version of the diagram and have them compare it with their answers.
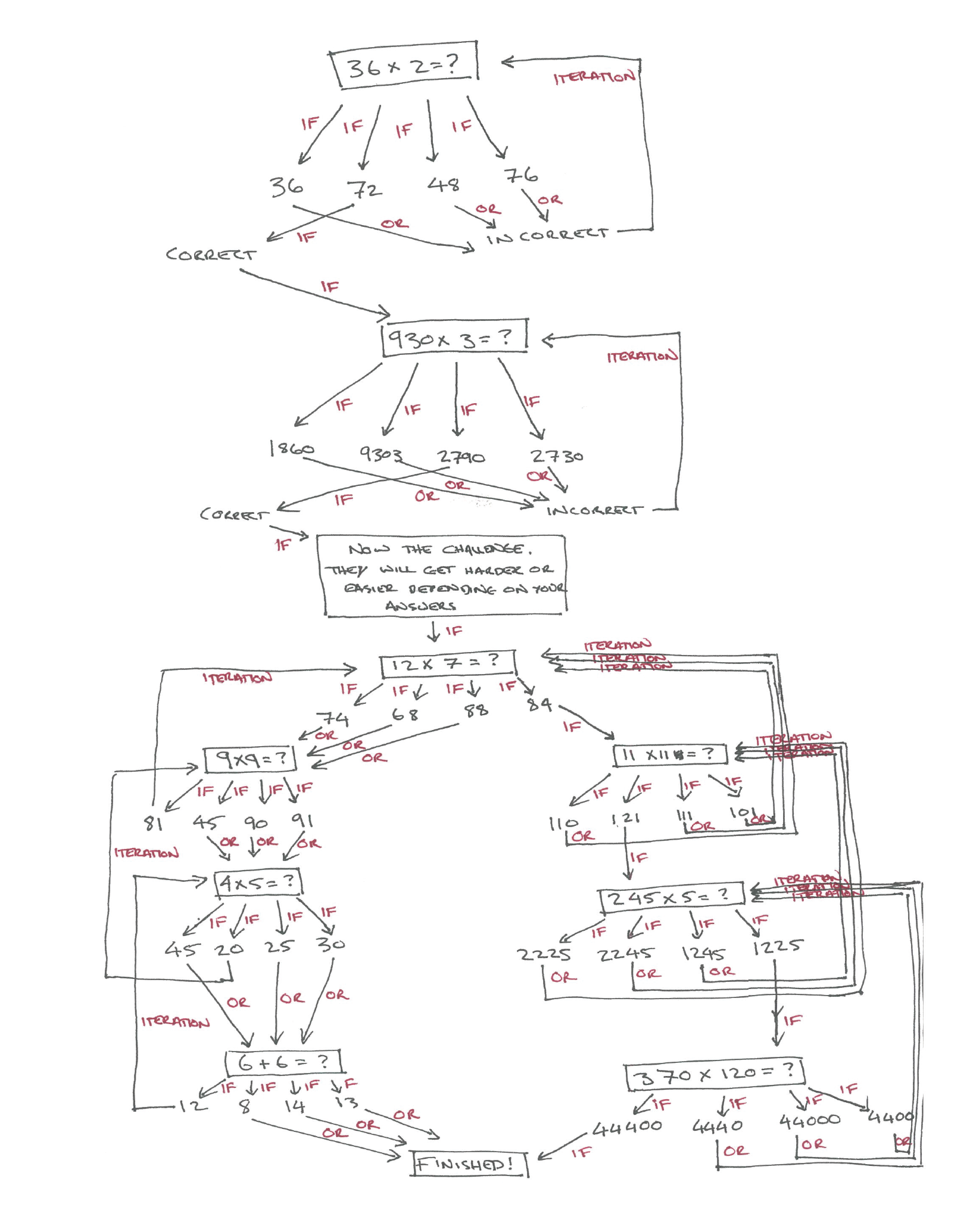
- There will be variations of answers that the students will have, some of which can still be considered correct. (For example, later in the diagram certain sections are listed as both an OR statement and an Iteration, students may have only one of these.)
- Emphasise that they are not to mark their diagram, that this is not about being 'right', but rather about finding out whether or not they understand the concepts.
- There will be variations of answers that the students will have, some of which can still be considered correct. (For example, later in the diagram certain sections are listed as both an OR statement and an Iteration, students may have only one of these.)
- Ask students whether they can think of any other ways that this quiz could have branched out.
- Lead them to the realisation that each right or wrong response could then branch off into another question, and that these questions could continue to branch.
- They do not need to iterate on every wrong response. Instead you could have an example where each time a question is answered correctly it branches to a slightly harder one, and each time it is answered incorrectly it branches to a slightly easier question. It doesn't need to loop back at any point if you do not want it to.
- Lead them to the realisation that each right or wrong response could then branch off into another question, and that these questions could continue to branch.
- Discuss any other ideas that they might have to extend the scope of the quiz.
Learning construction
- Explain to students that it is now their chance to create their own quiz.
- Explain that this is a maths quiz, but they can make it whatever kind of maths quiz they like.
- Do they want it to be multiplication? Division? Addition and subtraction? Fractions? It is up to them.
- Before they can actually create the quiz they need to create a planning diagram like the one they have just seen.
- Explain that they will be working in pairs and that it is a good idea if they brainstorm and discuss what they are thinking of doing before they begin their plan.
- Hand out two A3 pieces of paper per group, one for brainstorming and notes, and another for planning properly.
- Give the students time to start creating their quiz. Move around the room and help them, checking that they understand the relationships between the concepts.
Note: If students run out of space, which is very easy when dealing with branching concepts, simply give them some more paper to tape to the sides of their poster. - Fast finishers can attempt to extend their plans by adding further complexity and branches to their programs.
Learning demo
- Split the class into four different groups (aim for at least 3 pairs in each group). Explain that they are now going to test and share their quizzes.
- Have each pair give their plan to another group.
- When each group has another group's plan they take it in turns to read out the question and the possible answers.
- The other groups then answer, and follow the instructions on the plan to lead them to the next step.
Note: Before they begin, give each group a pad of sticky notes (or pieces of scrap paper and some sticky tape) and explain that each time they find a mistake, or something that doesn't work, they need to write it down on the sticky note and place it on the plan where they found the problem.
Learning reflection
After the students have finished trialing each others plans, ask them if there is anything that they would change or alter?
- Give groups 5 minutes to discuss whether or not their plan worked, or what might need to be changed to make it work more effectively.
- Explain they need to record these changes on their plan.